Strange Attractor Type V
The 3D system explores directly the variation of the number of wings without heavy techniques. To this end, we avoid generating multi-wing chaotic attractors with the bias of the complicatedness of heteroclinic loops, piecewise linear functions, or other advanced methods; as coupling 3D systems with additional first-order differential equations.
The multiplication of wings was controled solely by scalar parameters for both chaotic and regular dynamics.
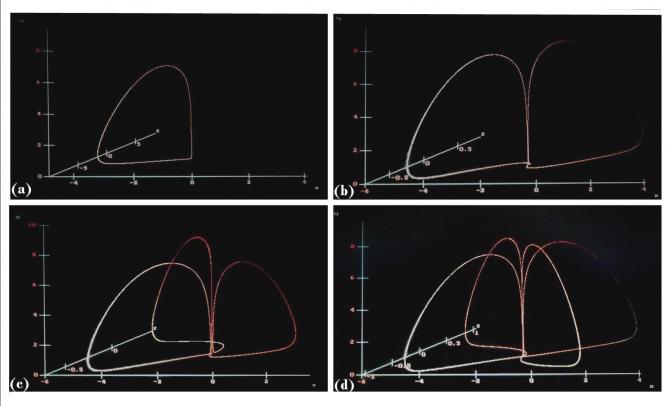
Fig. 1. Multi-wing Periodic Motions.
(a) A basic periodicity observed for P(α, β, µ)= (0.1, -0.1, 1), (b) period-4 dynamics for P(α, β, µ)= (0.1, 0.2, 0.7), (c) period-6 for P(α, β, µ)= (0.1, 0.1, 0.5), and (d) period-8 for P(α, β, µ)= (0.1, 0.1, 0.7).