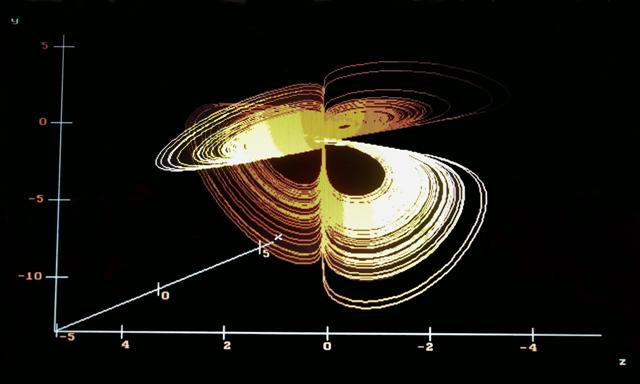
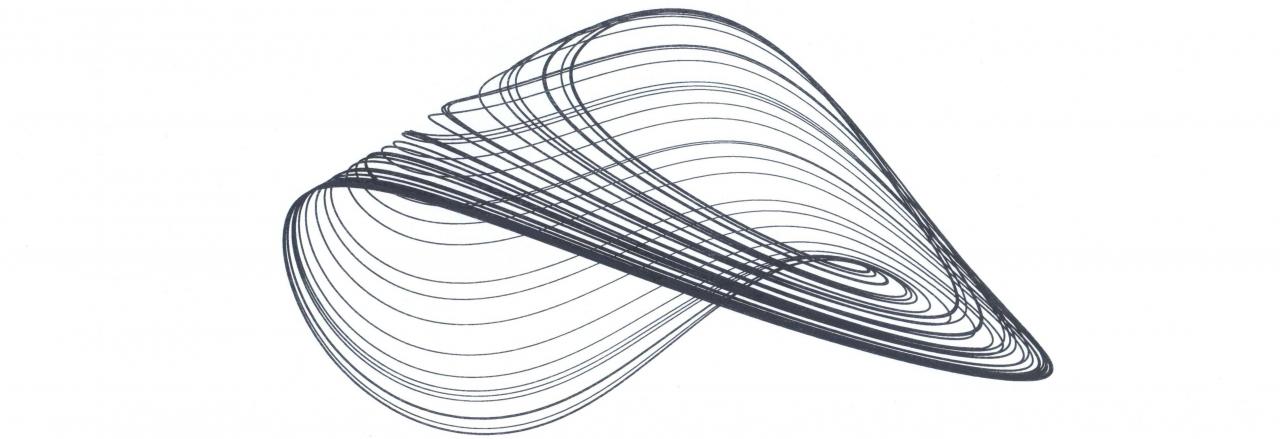
Strange Attractor Type IV

 

A Strange Attractor with a Swirling Scroll

 

The paper explores the morphological plasticity of the attraction basins of an asymmetric strange attractor with swirling scroll.

The system is governed by the following three-dimensional nonlinear differential equations:

dx/dt = α x ( y - 1 ) + β y z

dy/dt = φ ( 1 - x ² ) y + μ x z

dz/dt = η x y + s z 

For the set of parameters C0 (α, β, φ, μ, η, s) = (2, - 3, 0.8, 1, -2, 0.3), and the Initial Conditions (0.1, 0.1, 0.1)

an attractor appears in the upper phase space :

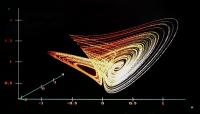
Besides for the same set of parameters C₀, and the negative Initial Conditions (-0.1, -0.1, -0.1)

another attractor appears in the lower phase space :

The two attractors are inversed position in the phase space (x, z, y):

 

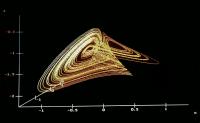
For the parameters C₂ (2, - 3, 0.8, 1, -2, 3) and the  IC (0.1, 0.1, 0.1 ) an attractor appears embodied in a basin utterly different from the first one:

 

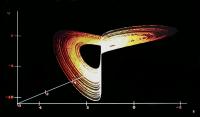
Besides, for the same parameters C₂ and the  negative IC (-0.1, -0.1, -0.1 ),

the attractor reappears in the opposite basin:

 

 

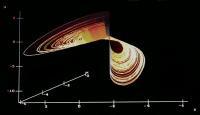
Eventually, the disposition of the two chaotic trajectories gathered in the same representation: