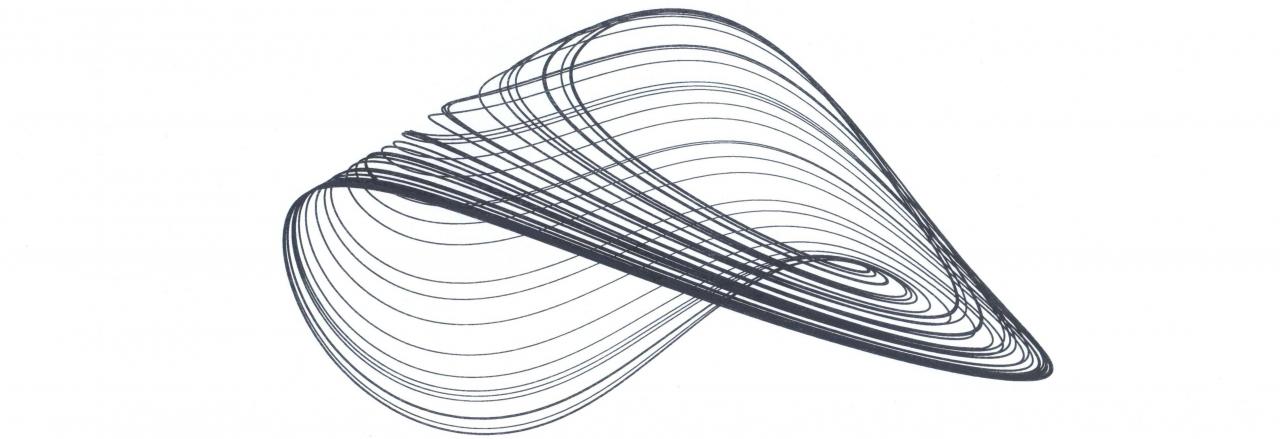
Strange Attractor Type I

In this system, we have "connected" a feedback loop (Equation 3) to a van der Pol oscillator in its extended formulation:

                              dx/dt = 0.02 y + 0.4 x ( 0.2 - y² )                   (1)

                              dy/dt = - x + s z                                            (2)

                             dz/dt = 10 x -  0.1 y                                       (3)

Indeed, this system apparently simple since it embeds only one nonlinear term, i.e. xy²  , simulates a wide range of dynamics when varying the parameter s.

Simple but so rich !

Furthermore, this chaotic system was implemented in a specific electronic device:

Chaotic attractor exhibited by the circuit for s = 50:

projections on the (a) X–Z and (b) Y–Z phase planes

The Circuit design and its characteristics are introduced in the paper:

Emulating complex business cycles by using an electronic analogue, co-authored by S. Bouali, A. Buscarino, L. Fortuna, M. Frasca, and L.V. Gambuzza, Nonlinear Analysis: Real World Applications, 13 (2012), pp. 2459–2465.

doi:10.1016/j.nonrwa.2012.02.010

 The PDF version available here:  nonlinear-analysis-bouali-et-al.pdf