ORCID iD: 0000-0002-4901-0221
Safieddine Bouali
PhD. in Economics, Habilitation,
Associate Professor,
University of Sfax,
Faculty of Economic Sciences and Management,
Airport Rd. 4, P 14, Sfax,
Tunisia
Current email adress: Safieddine.Bouali@isg.rnu.tn
Education:
PhD. in Theoretical Economics, University of Rennes 1, France, February 2001.
Master Degree in Economics, University of Tunis, Tunisia, December 1989.
Course presently taught:
*First Semester, 2023-2024
Microeconomics
______________________________________________________________________________________________
-Chaos Theory:
Historically, Edward Norton Lorenz established in 1963 the first strange attractor ever discovered. These amazing mathematical objects report chaotic dynamical patterns from deterministic equations. The related oscillations in a finite portion of time aren’t predictable and never resume a same path.
Strange attractors are they three-dimensional objects? Rather mathematical behaviors ! These are the displays of deterministic dynamics and cannot be summarized by a given frequency.
Explicitly oriented to the simplest exhibition of these dynamics, with very teensy mathematical tools, the purpose of this web-page aims to oversimplify to the young students the Chaos Theory.
In this e-page, we present our own research which led to new classes of 3D & 4D Strange Attractors.
See menu for further technical details and also beautiful pictures created by the Mathematics & Art pathfinder : Jos Leys.
-Network Economics:
We present also our own research on the Tunisian Telecommunication Market.
- Economics under the Covid-19 Threat:
The current pandemic could expand oppotunistic ploys between firms ! We present below a paper on the ability of the contractual theory to prevent such exploitative practices.
I. 3D Strange Attractors
The chaotic dynamics are non-standard flots, but can be represented in finite phase spaces.
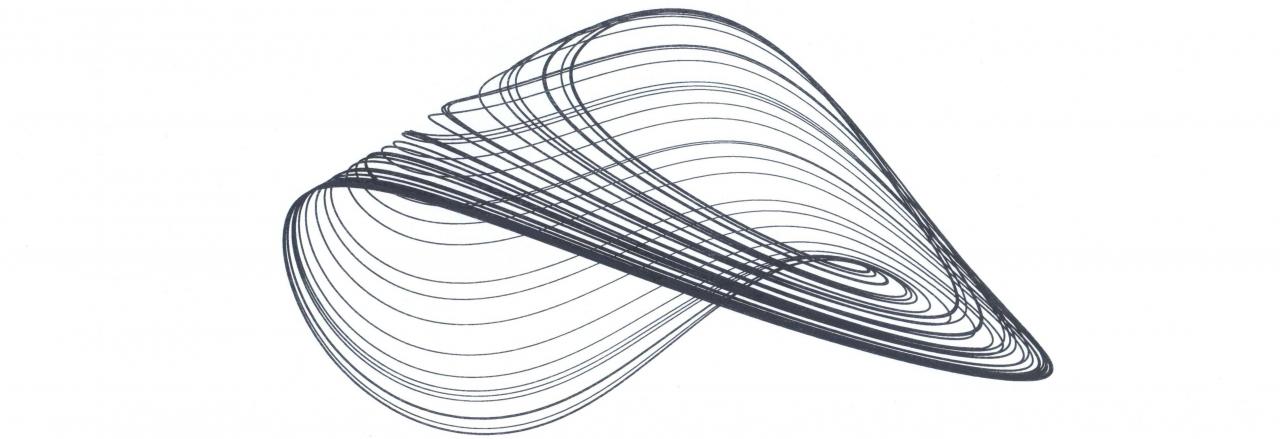
1/ Strange Attractor Type I :
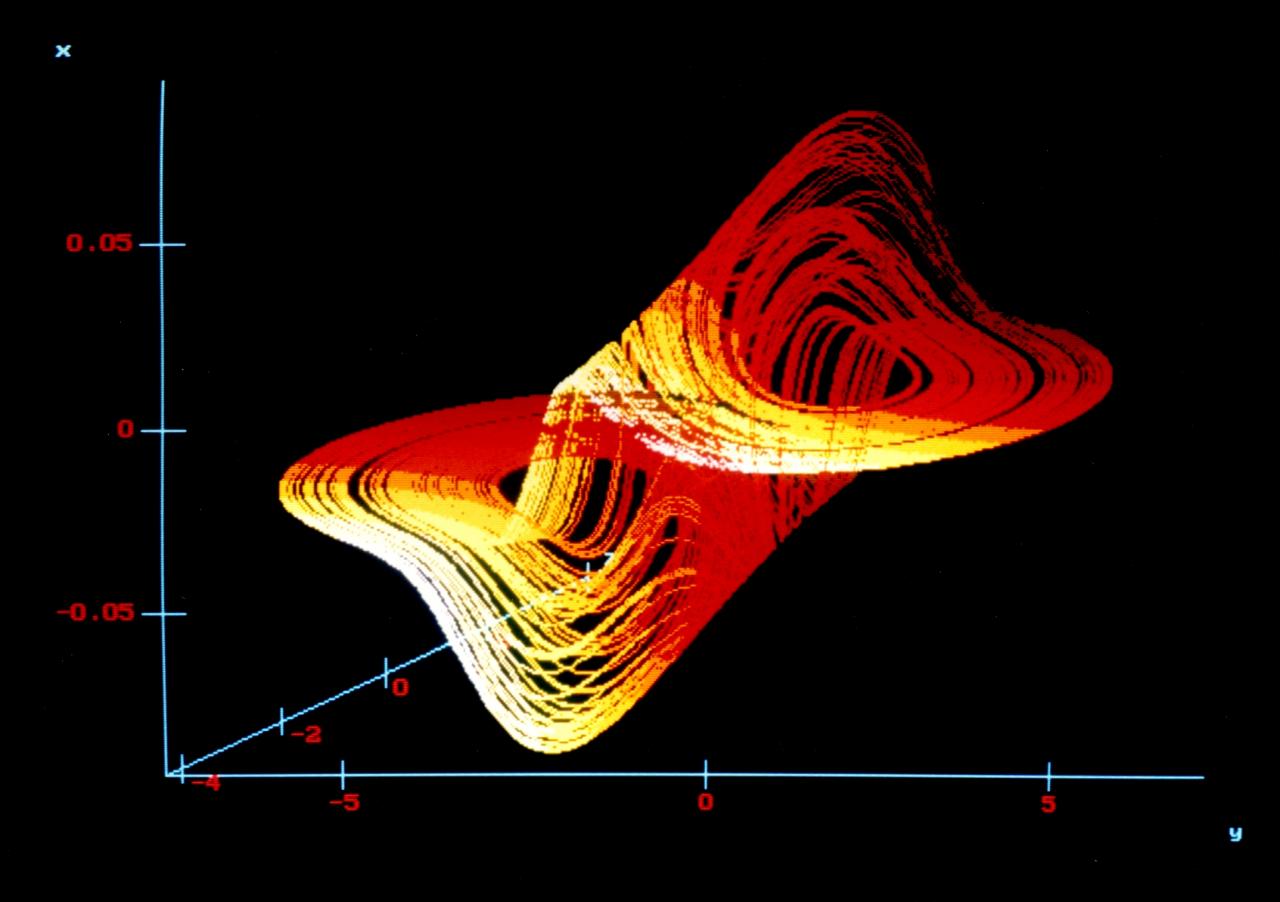
(a)
Fig .1. (a) Phase portrait of the strange attractor, and (b) its representation with a change in the control parameter
in (-y, x, z) system of axis
The related paper was published in the International Journal of Bifurcation and Chaos (1999), 9, 4, 745-756:

The PDF version available here:  Bouali Safi-Chaos
Bouali Safi-Chaos
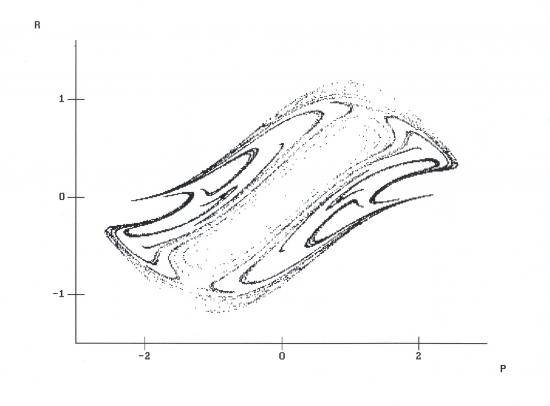
The chaotic model illustrates the paradoxical profit motion of a compagny when it adopts a strict self-discipline of the dividend payoff (see Arxiv preprint (2002) : The Hunt Hypothesis and the Dividend Policy of the Firm. The Chaotic Motion of the Profits).
Fig 2. Poincaré Map of the chaotic motion of profits . Axis of the deux variables: Profits and reinvestments .
Such "Sculptures of Chaos" are presented and simulated in an e-paper co-authored with Jos Leys at the site "Images des Mathématiques", affiliated to the CNRS, France:
Fig. 3. Screenshot of the online paper.
It includes for example such two elegant figures :

Fig. 4. Starting from two different initial conditions, simulations
of the dynamical system converge to the same attractor.
Fig. 5. For a particular parameters, the system leads to two attractors
in separate basins even from close initial conditions..
Here, a YouTube animation by the wizard of Mathematical Imagery Jos Leys :
*
New !
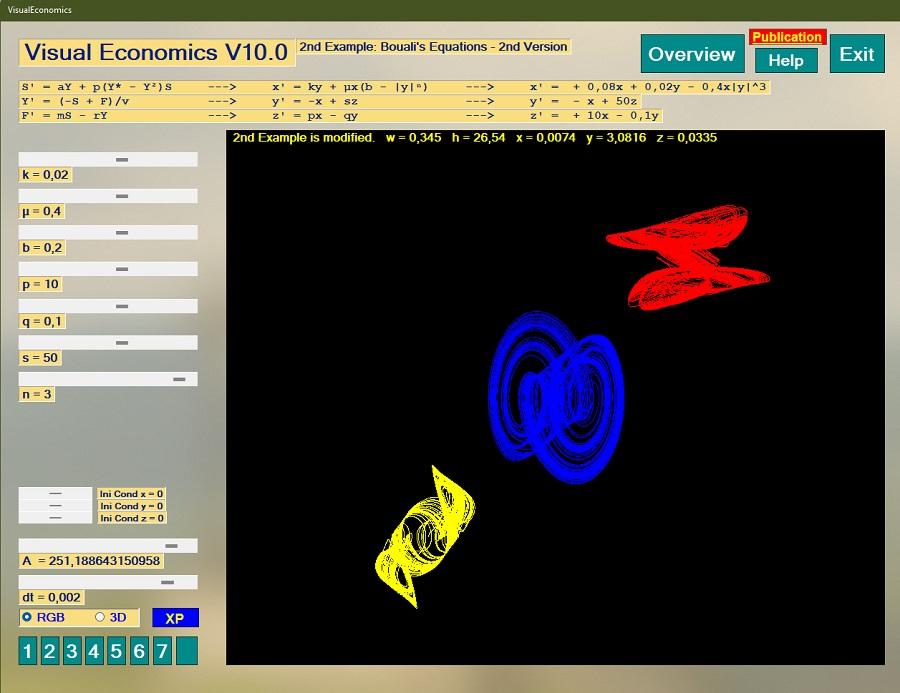
Simulation with VisualEconomics, an application made by Gert Hohndorf.
( Redirection to the App. by clicking on the screenshot)
Fig. 6. Modifying parameters, several shapes of the strange attractors could be created !
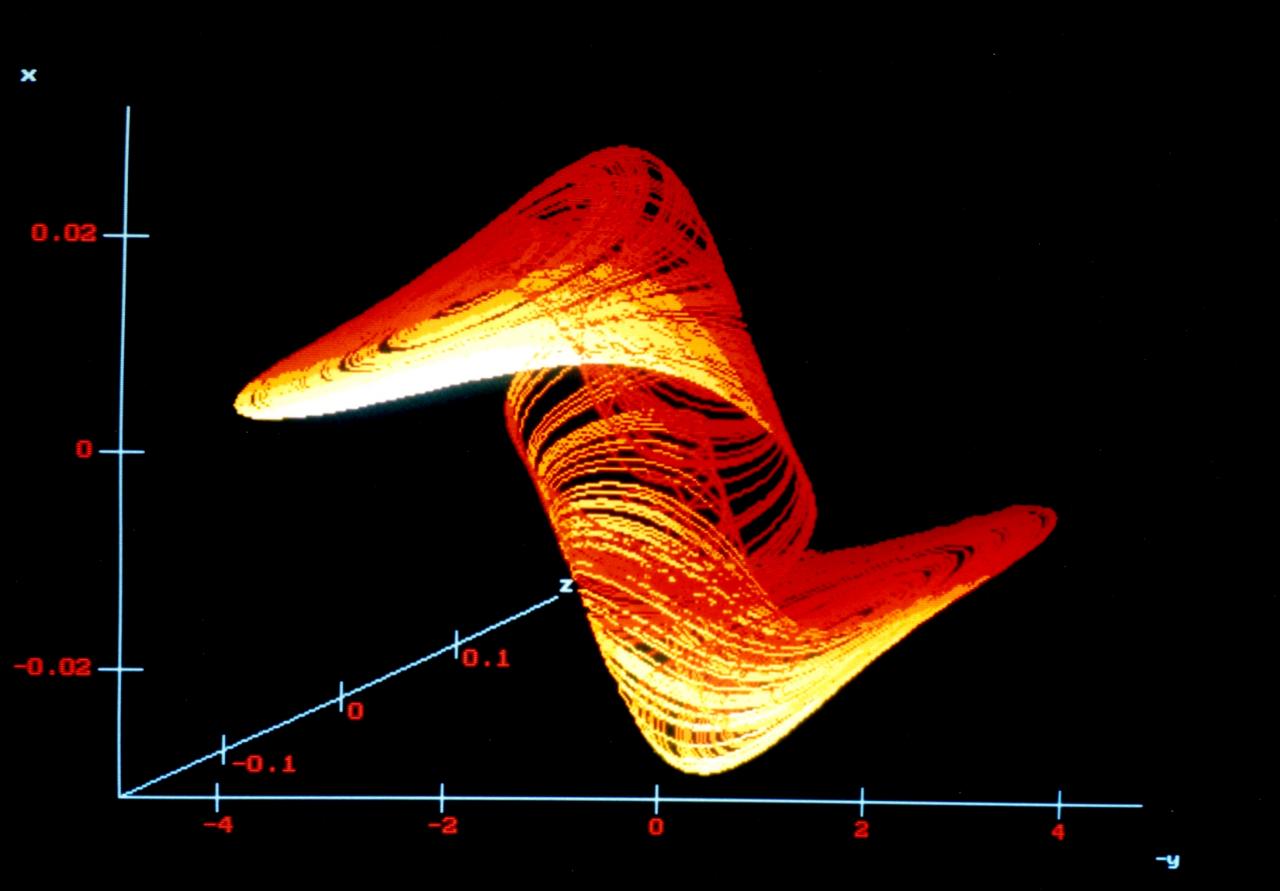
2/ Strange Attractor Type II :

The research paper was published in Nonlinear Dynamics (2012), 70, pp. 2375–2381.
DOI 10.1007/s11071-012-0625-6
The PDF version available here: nody2.pdf
nody2.pdf
Simulation and Animation by the Mathematical Imagery pathfinder Jos Leys :
3/ Strange Attractor Type III :
Fig.1. Phase portrait of the Strange Attractor Type III
The preprint:
A 3D Strange Attractor with a Distinctive Silhouette. The Butterfly Effect Revisited
A Mathematical Imagery and Simulation Designed by the Maths & Arts creator Jos Leys :
4/ Strange Attractor Type IV :

Phase Portrait of the Attractor Type IV
The paper :
Basins of Attraction Plasticity of a Strange Attractor with a Swirling Scroll
A beautiful simulation of the Attractor 4 "solo" made by Jos Leys :
Simultaneous simulations of the two attractors in their respective basins by Jos Leys :
5/ Strange Attractor Type V :
The e-print:
A Versatile Six-wing 3D Strange Attractor
A new intentionally constructed model exhibiting double, four- or even six-wing strange attractor is investigated. We point out that under the influence of the scalar parameters, such versatile chaotic attractors are obtained.
The model presentation with simulations of the double-, four- and six-wing attractor in the following ( beautiful !) film made by Jos Leys:
II. 4D Chaotic Attractors
The e-print HAL, archives.ouvertes.fr:
Strange Attractor Morphogenesis by Sensitive Dependence on Initial Conditions
It is acknowledged that a strange attractor is locally unstable but globally stable. Our experiementation displays that strange attractors could be unstable at all scales. Coexistence of distinct strange attractors found not by the modification of an unique or several parameters but surprisingly by slight initial condition changes.
The 4D system:
x, y, z, and v, state variables.
It is expected that such system converges asymptotically to an unique strange attractor for any initial conditions. However, the following portraits projected to the (x, y, z) phase space are related to small changes of these conditions:
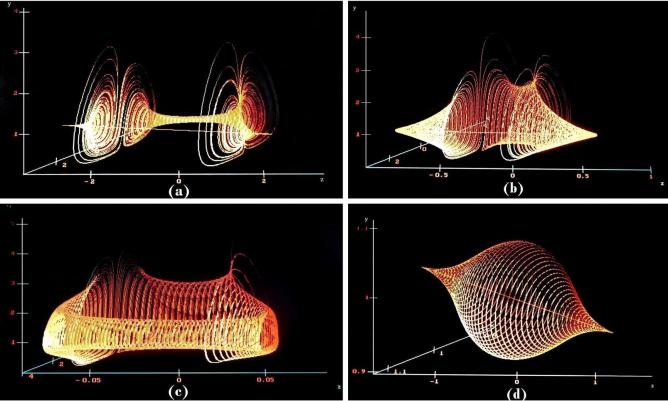
(a) A typical morphology obtained for ICa=( xa, ya, za, va)= (2, 2, 2, 2), (b) Another distinct morphology obtained for ICb=( xb, yb, zb, vb)= (0.5, 0.5, 0.5, 0.5), (c) A more complex morphology obtained for ICc=( xc, yc, zc, vc)= (0.05, 0.05, 0.05, 0.05), and (d) A Lemon-like shape for ICd=( xd, yd, zd, vd)= (1, 1, 1, 1).
Figure 1. Morphological Plasticity of the Phase Portraits
Such sensitive dependence on initial conditions is illustrated in this simulation, Bouali attractor 4D - Morphogenesis, by Jos Leys:
____________________________________________________________________________________________________________________________________________________________
III. Hyperchaotic Attractors
The Science of Process mixing order and disorder can be extended to the space of dimension four. Here too there are strange attractors !
1/ Hyperchaotic 4D Strange Attractor A:
 (a)
(a) (b)
(b)
 (c)
(c) 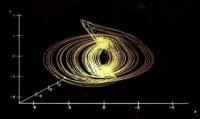 (d)
(d)
3D projections of the 4D Hyperchaotic Attractor
(a), (b), (c), and (d) are part views of the Attractor since the overall
representation of the 4D space is unrealizable
The paper:
A New Hyperchaotic Attractor with Complex Patterns
An artistic animation by the maths & Arts pathfinder Jos Leys :
2/ Hyperchaotic 4D Strange Attractor B:
(a) (b)
(b)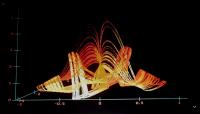
(c) (d)
(d)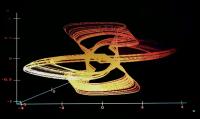
3D projections of the phase portrait of the Attractor
(a), (b), (c), and (d) are the different representations
of the Hyperchaotic Attractor
The paper :
A Novel 4D Hyperchaotic Attractor with Typical Wings
Awesome simulation and Animation by Jos Leys :
***
The article "Hidden Structure and Complex Dynamics of Hyperchaotic Attractors",
analyzing the two hyperchaotic systems is published in:
Annual Review of Chaos Theory, Bifurcations and Dynamical Systems, Vol. 6, pp. 48-58.

Cover images, figures and graphics of the paper are kindly provided by Jos Leys.
A pre-print on strange attractors ...which should not exist !
"Discovering the Beauty of False Strange Attractors"
march 2021, DOI:10.13140/RG.2.2.32948.37767
co-authored with Marcus A. Rezende, and Jos Leys
Abstract:
In this paper we present a simple method to discover singular silhouettes having chaos attributes. The method rearranges in an arbitrary way the coordinate series of known strange attractors.
Reconnecting arbitrarily such series, the method leads to a novel sequence of stretch & fold, the fundamental kinematics of the attractor strangeness. The intersection of Mathematics & Arts being the main focus of this research, strange attractors that should not exist were generated displaying a facet of creative processes in visual arts. The portraits, sometimes elegant among the dozens that the
application allows to build, unveil false strange attractors. By performing harmonious or disturbedcarves, our application of generative art can create silhouettes not seen before.
Key words: Maths & Arts, Generative Art, Stretch & Fold Kinematics, Strange Attractors, Discovery Process

Even though false attractors shouldn't exist, Jos Leys simulate them !
________________________________________________________________________________________________________________________________________________________________________
-Complex Systems:
In a wide range of nonlinear phenomena, dynamical behavior can be suitably formulated with differential equations.
We explored also theoretical fields far from our Economics Education.
Tropical Cyclone Dynamics:

Idealized Tropical Cyclone; Aerological circulation follows a quasi-torus structure
(front slice removed to display its internal structure).
Coauthored paper by:
Safieddine Bouali and Jos Leys (2013): "Tropical Cyclone Genesis: A Dynamician’s Point of View", pp. 187-192, in:
Proceedings of the 4th International Interdisciplinary Chaos Symposium
Stavrinides, S.G., Banerjee, S., Caglar, S.H., Ozer, M. (Eds.)
2013, XV, 581 p. 236 illus.

link:
http://www.springer.com/physics/complexity/book/978-3-642-33913-4
-Network Economics
We studied the competition of the mobile network operators in the Tunisian market of telecommunications:
1/ "Regulated termination rates and competition among Tunisian mobile network operators. Barriers, bias, and incentives",
Telecommunications Policy, 41 (2017), 573–586.
To Download :![]() Sbouali tpy (1.36 Mo)
Sbouali tpy (1.36 Mo)
Abstract:
Since 2006, the Tunisian National Regulatory Authority has been imposing multiannual mobile-to-mobile termination rates, first on the duopoly of Tunisie Télécom and Tunisiana, and then on all three providers once Orange Tunisie entered the market in 2010.
This research studies the interplay between interconnection rates for mobile call termination and the retail price competition for prepaid SIM cards, predominantly chosen by Tunisian consumers. We show that the duopoly was practicing “price alignment” for off-net calls, and that subsequently, the third provider entering the market sparked a decisive initial price drop associated with the non-reciprocal rate it enjoyed.
However, the price war, which benefited consumers, only occurred when the Regulatory Body eliminated differential tariffs between on and off-net calls in the retail market. It follows that, everything else being equal, an interconnection rate drop alone will not lead to a decrease in retail prices.
-------------------------------------------
2/ "Price-cuts for the Mobile Voice Calls and the Tit-For-Tat Game on the Tunisian Telecommunication Market", 2021, 6 , Issue 1, p. 64-75.

Abstract:
The Tunisian telecommunication market experienced intense price-cuts of the mobile-to-mobile voice phone services throughout the 2011-2015 period. This paper shows that the three major providers, Tunisie Télécom, Ooredoo and Orange, have replicated the price-cuts as in the Tit-For-Tat game or over-reacted despite the hurt of their revenues. This paper investigates whether price dynamics is a simple strategy for gaining market share or a “price war”, as described in the economic literature. This paper constructs the demand curves for each provider based on price-elasticity, average revenue per user and price series, and then we analyze their lags. The pure pricing strategy is discussed as it coincided with the fast growth of data traffics and the decrease of the gross national disposable income per capita.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
New ! Covid-19 Impact on Vertical Relations
A Research Paper on Opportunistic Conduct between Firms, and Unleashed by the Covid-19 Pandemic:
Covid-19 Pandemic and Opportunism. Short-run Market Vulnerability and Exploitative conduct
in the Journal of Research in Business and Management, Volume 8 ~ Issue 7 (2020) pp. 01-10.

-------------------------------------------------------------------------------------------------------------------------------------------------
--------------------------------
The visit counter was previously reset when it exceeded 8,000.