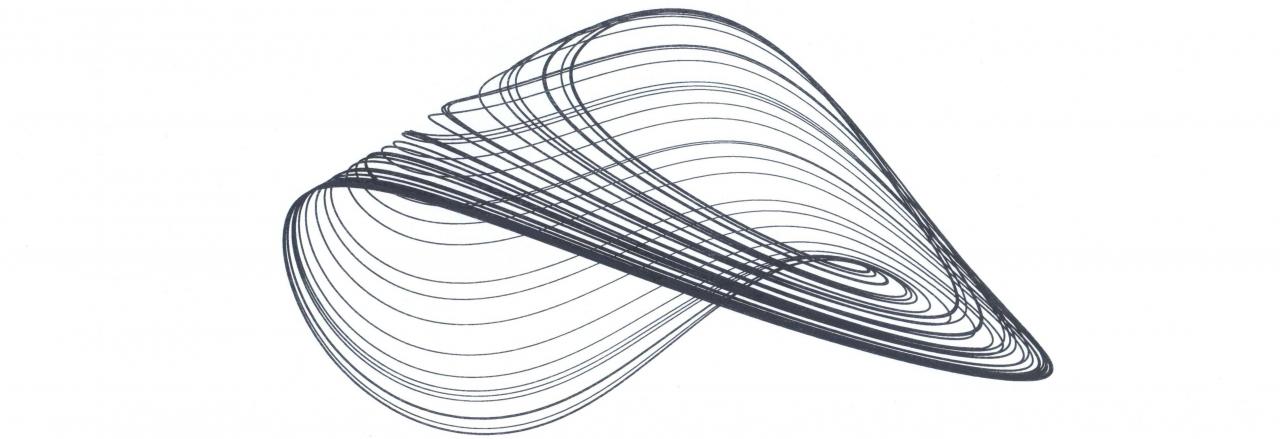
4D Chaotic Attractor

A Collection of Attractors with Distinct Morphologies

We simulate a 4D system keeping unchanged the P parameters and all the graphical representations of the trajectories will be projected within the (x, y, z) space. 

Surprisingly, the space portraits depict a noteworthy morphological variety of shapes even if the system and the values of its parameters are kept unchanged. A non-standard butterfly effect is highlighted.

The model contradicts the Butterfly Effect as the most blazing legacy of the wide scientific contribution Edward Norton Lorenz (1963). The SDIC reports that a small gap between two initial conditions in its idealized meteorological system deflects their paths in a way that no prediction of their drift could be done. Indeed, their gap grows at exponentially distance. Such singular phenomenon states that a strange attractor is locally unstable. However,  it is globally stable since the trajectories converge to the same attractor. 

The main outcome of our paper is precisely that a strange attractor is not only locally unstable but also it could be globally unstable leading to another attractor by a simple modification of the initial conditions.